문제 요약
- 알고리즘 분류: 구간합, 누적합, 수학
- 난이도: Gold3
- 문제내용:
- N개 수와 연속적인 구간의 합이 M인 개수를 구해하
- 사이트 : https://www.acmicpc.net/problem/10986
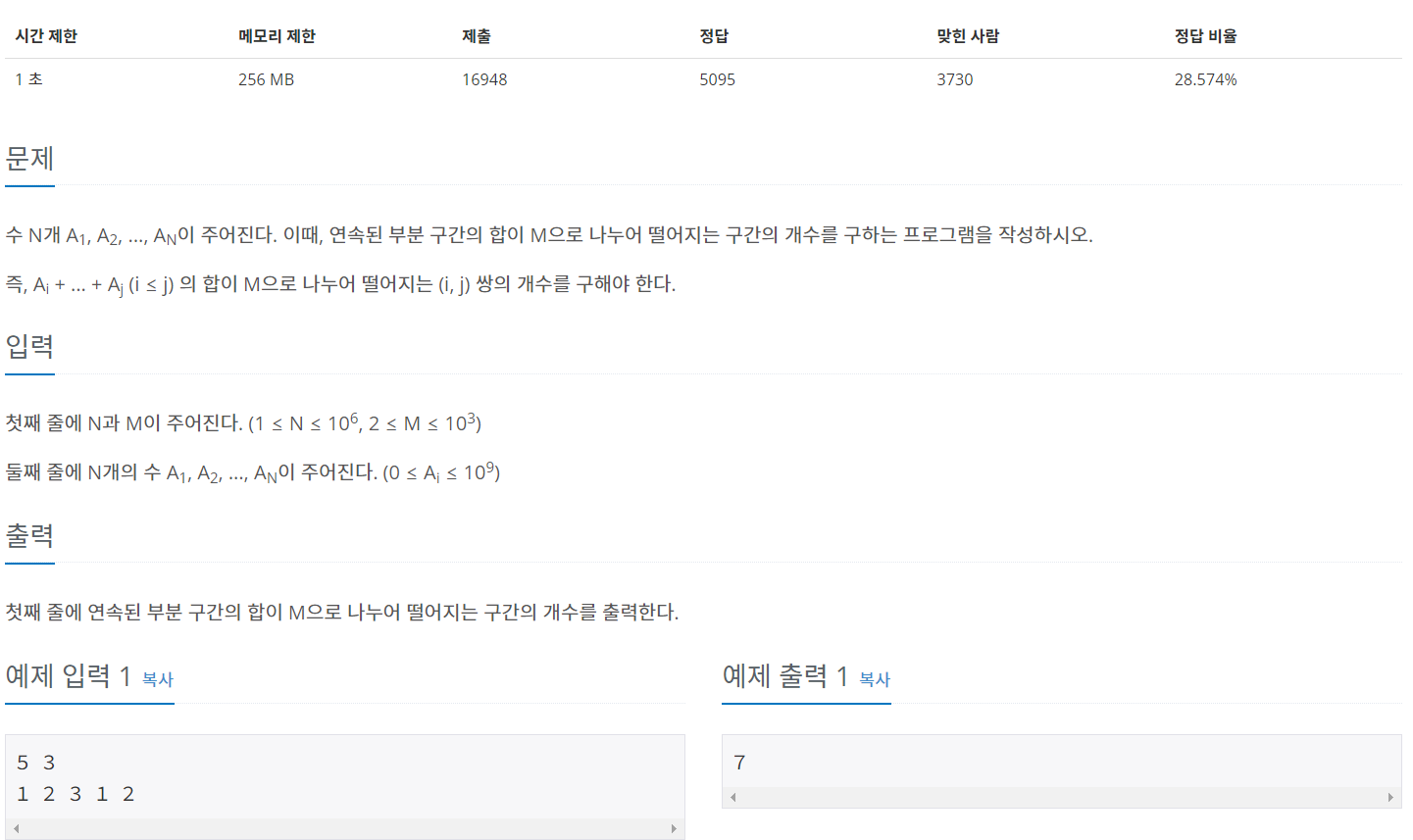
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
문제풀이
이번문제는 구간합에서 응용한 문제이다. 구간합에 대한 이론은 아래의 사이트에 참조하면 된다.
https://jih3508.tistory.com/50
[알고리즘 이론] 구간합, 누적합(prefix sum)
이론 1차원 배열 누적합 누적합부터 먼저 설명하면 0번째 인덱스 부터 N 번째 인덱스까지 탐색하면서 인덱스 i일때 0번째 인덱스 부터 0번째 인덱스합을 말한다. Python array = [1, 8, 7, 4, 3, 5, 6] n = len
jih3508.tistory.com
문제 접근방법
N, M = map(int, input().split())
A = list(map(int, input().split()))
prefix_sum = [0]
for i in range(N):
prefix_sum.append(prefix_sum[i] + A[i])
count = 0
for i in range(1, N + 1):
for j in range(i):
count += (prefix_sum[i] - prefix_sum[j]) % M == 0
print(count)구간합을 응용하는 문제인데 구간합을 안다고 쉽게 위 코드 처럼 풀면 시간초과가 나올것이다. 그 이유는 수열의 개수가 1,000,000 데이터이다. 위 코드에서 누적합의 차이 구한다고 이중 for문 사용하면 O(N^2) 시간복잡도가 나와서 안된다.
그래서 O(N)으로 풀어야 하는데. 방법은 조합이론으로 풀것이다.

위 그림은 문제 예제에서 표로 정리한것이다. 누적합에서 나머지 3의 결과를 보면 0이 3개이고 1이 한개 2는 없다.
나머지의 개수를 밑에 표로 다시 정리했다.

이제 나머지 개수를 가지고 조합 이론을 적용 시킬것이다. 일단 먼저 나머지 이론중에서
A MOD N - B MOD N = (A - B) MOD N
위 이론을 먼저 생각 해야 한다. 즉, 나머지 같은것 2개를 빼면 0이다. 예시로 0번째 인덱스 누적합과 3번째 인덱스 누적합은 1이다. 여기서 1 ~ 3 번째 구간합에서 나머지 3하면 0이 나오고 3번째 인덱스 누적합과 0번째 누적합 빼서 나머지 3하면 0이다. 즉, 같은것을 빼면 0이기 때문에 각 다른 구간이고 나머지가 같은것 2개만 뽑으면 되서 조합을 적용만 하면 끝이다.
이제 접근 하는 방법을 알았으니 총 합을 구하면 되는데 조합한 결과와 나머지가 0인 개수만 더하면된다. 나머지가 0인 개수를 더해줘야 이유는 조합은 구간합이 0일때만 구하는 것이지만 누적합이 0일때의 경우도 더해줘야 하기 때문이다.
정리
- 처음에 누적합과 나머지가 나올수 있는 수를 나타내는 배열을 선언한다.
- 누적할때마다 나머지 부분에 개수를 추가해라
- 개수를 구할 변수를 초기화하고 초기값은 누적합에서 나머지가 0의 개수이다.
- 나머지가 0 부터 M - 1까지 각 조합의 값을 추가한다.
Code
Python
N, M = map(int, input().split())
A = list(map(int, input().split()))
prefix_sum = 0
divided = [0] * M
for i in range(N):
prefix_sum += A[i]
divided[prefix_sum % M] += 1
count = divided[0]
for i in divided:
count += i * (i - 1) // 2
print(count)Java
개수 세는 부분은 Integer의 범위가 넘어 갈수가 있어서 Long 타입으로 처리해야 한다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] divided = new int[M];
int prefix_sum = 0;
st = new StringTokenizer(br.readLine());
for(int i = 0; st.hasMoreElements(); i++) {
prefix_sum =(prefix_sum + Integer.parseInt(st.nextToken())) % M;
divided[prefix_sum]++;
}
// 답이 Integer 보다 범위가 클수 있어서 Long타입으로 선언한다.
long count = divided[0];
for(int i : divided) {
count += (long) i * (i - 1) / 2;
}
System.out.println(count);
}
}'알고리즘 > 백준' 카테고리의 다른 글
| [BAEKJOON] 6810 ISBN (0) | 2022.11.13 |
|---|---|
| [BAEKJOON] 2587 대표값2 (0) | 2022.11.12 |
| [BAEKJOON] 11660 구간 합 구하기 5 (2) | 2022.11.10 |
| [BAEKJOON] 2566 최댓값 (0) | 2022.11.09 |
| [BAEKJOON] 16139 인간-컴퓨터 상호작용 (0) | 2022.11.09 |



