이론
1차원 배열
누적합
누적합부터 먼저 설명하면 0번째 인덱스 부터 N 번째 인덱스까지 탐색하면서 인덱스 i일때 0번째 인덱스 부터 0번째 인덱스합을 말한다.
Python
array = [1, 8, 7, 4, 3, 5, 6]
n = len(array)
prefix_sum = [0] * n
for i in range(n):
for j in range(i+1):
prefix_sum[i] += array[j]Java
import java.util.Arrays;
public class Main {
public static void main(String[] args){
int[] array = {1, 8, 7, 4, 3, 5, 6};
int n = array.length;
int[] prefixSum = new int[n];
for(int i = 0; i < n; i++) {
for(int j = 0; j <= i; j++) {
prefixSum[i] += array[j];
}
}
}
}JavaScript
const array = [1, 8, 7, 4, 3, 5, 6];
const size = array.length;
let prefixSum = new Array(size).fill(0);
for (let i = 0; i < size; i++) {
for (let j = 0; j <= i; j++) {
prefixSum[i] += array[j];
}
}위 코드 처럼 표현을 할수 있고 sum이라는 함수를 사용해서 구할수 있다. 하지만 위 코드 처럼 사용 할시에는 O(N^2) 시간 만큼 걸린다. 하지만 밑에 방식으로 할 시에는 O(N)으로 처리가 가능하다.
Python
array = [1, 8, 7, 4, 3, 5, 6]
n = len(array)
prefix_sum = [0] * (n + 1)
for i in range(n):
prefix_sum[i + 1] = prefix_sum[i] + array[i]Java
public class Main {
public static void main(String[] args){
int[] array = {1, 8, 7, 4, 3, 5, 6};
int n = array.length;
int[] prefix_sum = new int[n + 1];
for(int i = 0; i < n; i++) {
prefix_sum[i + 1] = prefix_sum[i] + array[i];
}
}
}JavaScript
const array = [1, 8, 7, 4, 3, 5, 6];
const size = array.length;
let prefixSum = new Array(size + 1).fill(0);
for (let i = 0; i < size; i++) {
prefixSum[i + 1] = prefixSum[i] + array[i];
}몇번째 인덱스 까지 합친것을 부를 때 index 위치에 있는 값만 부르면 된다.
구간합
누적합에 대한 개념이 들어왔으면 구간합은 누적합 구간간의 차이만 빼면 된다.

위 표를 보면 배열과 누적합의 결과를 표로 나타 낸것이다. 예시로 2번째 인덱스와 5번째 인덱스 합을 구해 보겠다.
그냥 코드로 index 2번째 부터 5번째까지 for문으로 돌리면 되지만 그러면 시간이 O(N) 만큼 나간다. 하지만 누적합의 차를 구하면 O(1)만큼 걸린다. index 탐색해서 구하는 것과 구간합 구한 후에 비교 해보면 7 + 4 + 3 + 5와 28 - 9를 비교해보면 구간 합이 더 간다한것을 알 수가 있다.
이제 구간합의 공식을 보면 2번째 부터 5번째 합인데 구간합에서는 5번째와 1번째 차이를 보았다. x, y(x < y) 라고 가정할때 구간합은 prefix_sum[y] - prefix_sum[x-1] 로 결론이 날 수 있다. 하지만 0번째 부터 N 까지 구하면 인덱스 초과가 날수 있어서 밑에 그림과 같이 맨앞에 0을 추가 해야 한다.

구간 합의 코드
위에 설명을 아래 코드로 표현 한것이다. 코드는 누적합 구하는 코드와 누적합 저장하는 배열에 맨 앞에 0을 추가하는것 말고 없다.
Python
array = [1, 8, 7, 4, 3, 5, 6]
n = len(array)
prefix_sum = [0] * (n + 1)
x, y = 1, 5
for i in range(n):
prefix_sum[i + 1] = prefix_sum[i] + array[i]
part_sum = prefix_sum[y] - prefix_sum[x - 1]Java
public class Main {
public static void main(String[] args){
int[] array = {1, 8, 7, 4, 3, 5, 6};
int n = array.length;
int[] prefix_sum = new int[n + 1];
int x = 1;
int y = 5;
for(int i = 0; i < n; i++) {
prefix_sum[i + 1] = prefix_sum[i] + array[i];
}
int part_sum = prefix_sum[y] - prefix_sum[x - 1];
}
}JavaScript
const array = [1, 8, 7, 4, 3, 5, 6];
const size = array.length;
let prefixSum = new Array(size + 1).fill(0);
const x = 1
const y = 5
for (let i = 0; i < size; i++) {
prefixSum[i + 1] = prefixSum[i] + array[i];
}
const partSum = prefixSum[y] - prefixSum[x-1]마무리
위 그림 설명을 1차원 배열 구간합, 누적합을 그림으로 표현하면 아래와 같다.
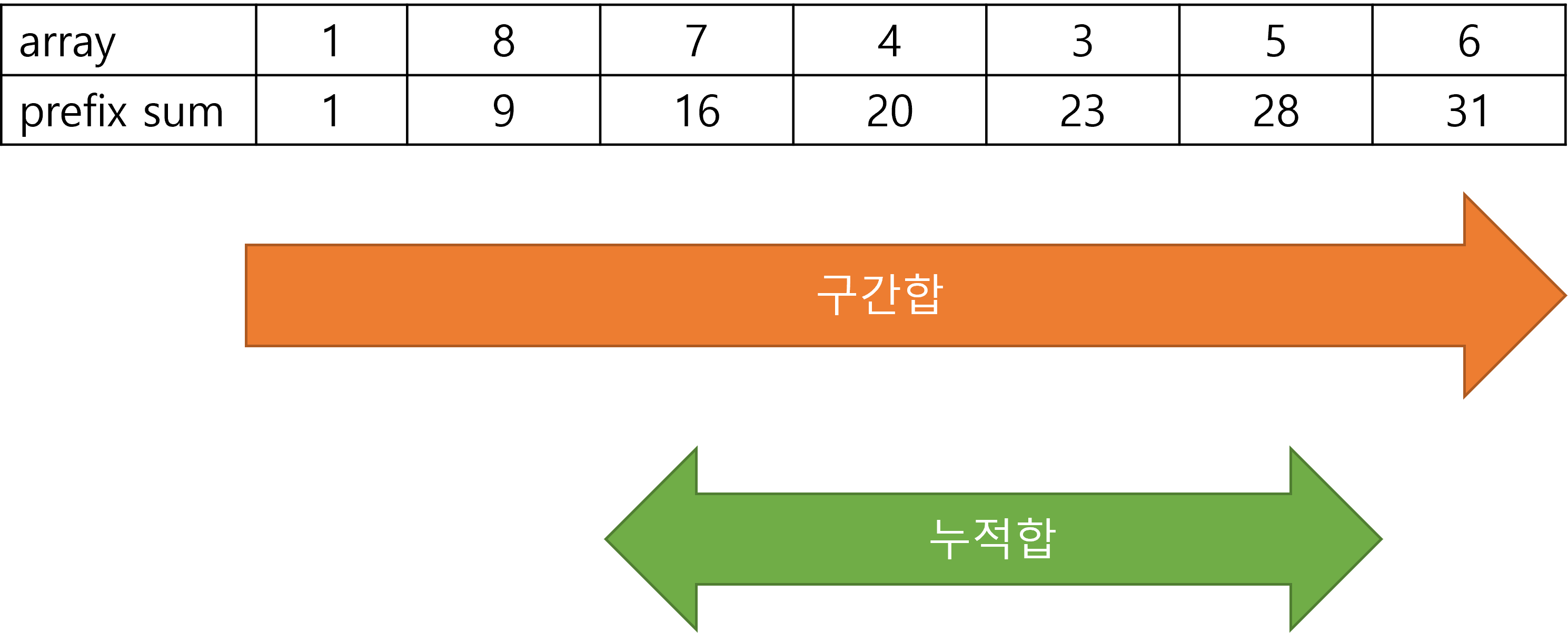
1차원 구간합, 누적합 추천 문제
문제: 수열
난이도: 하
https://www.acmicpc.net/problem/2559
2559번: 수열
첫째 줄에는 두 개의 정수 N과 K가 한 개의 공백을 사이에 두고 순서대로 주어진다. 첫 번째 정수 N은 온도를 측정한 전체 날짜의 수이다. N은 2 이상 100,000 이하이다. 두 번째 정수 K는 합을 구하기
www.acmicpc.net
문제: 구간 합 구하기 4
난이도: 하
https://www.acmicpc.net/problem/11659
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
2차원 배열
누적합
1차원 배열이랑 비교하면 좀 복잡 할 수가 있다. 1차원 배열 누적합은 이전 값을 저장 하는 식은데 2차원 배열은 위에 값하고 왼쪽 값이랑 더 하기만 하면 안된다. 거기에 집합의 성질은 합집합의 성질에 의해서 공통 되는 부분은 제거하는 작업해서 계산식이 좀 복잡할수가 있다.
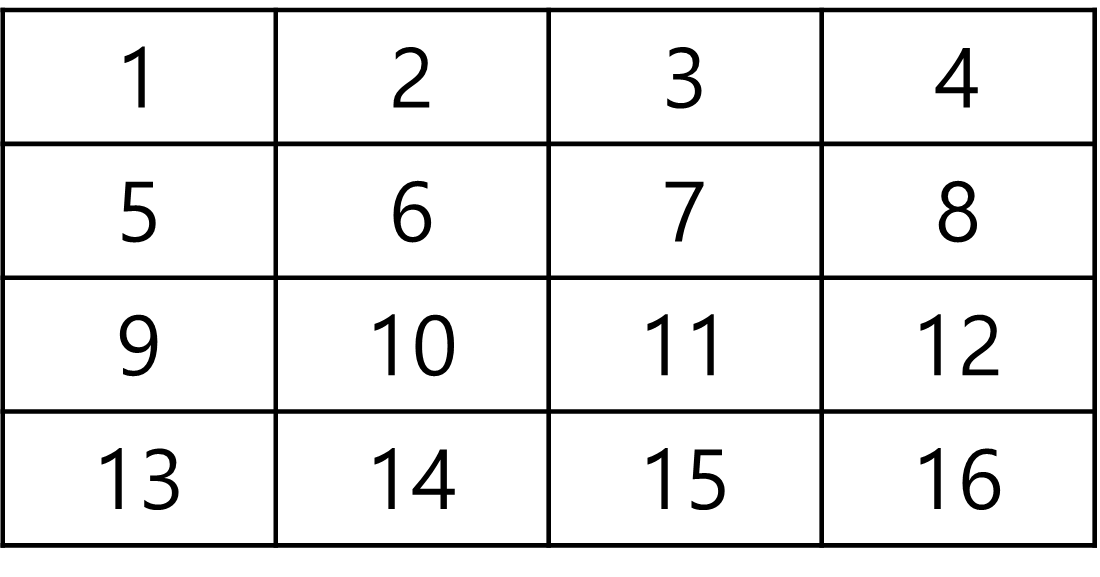
위 그림으로 2차원 배열로 예시로 한 표이다. 가로, 세로 0번째 인덱스는 이전 행과 열을 더 해서 추가하면 쉽지만 (2 ~ 4, 2 ~ 4)의 누적합은 자신 인덱스의 위, 왼쪽을 추가만 하면 되지 않는다.

왼쪽 그림은 1번째 행열 누적합 연산한 결과이다. 예시로 (2, 2)를 예제로 하겠다. 기존 계산 방법으로 (2, 2) 누적 합은 1 + 2 + 5 + 6 = 14이다. 기존 누적 합으로 위 아래만 계산하면 3 + 6 + 6 = 15가 나온다. 계산이 잘못 된 이유는 이전 왼쪽과 위이전 쪽이랑 공통된 부분까지 연산해서 생긴 결과이다. 그래서 공통된 부분을 제거를 해야한다. 공통된 부분을 제거할 부분은 (1, 1) 다신 연산을 하면 3 + 6 + 6 - 1 = 14가 나온다.
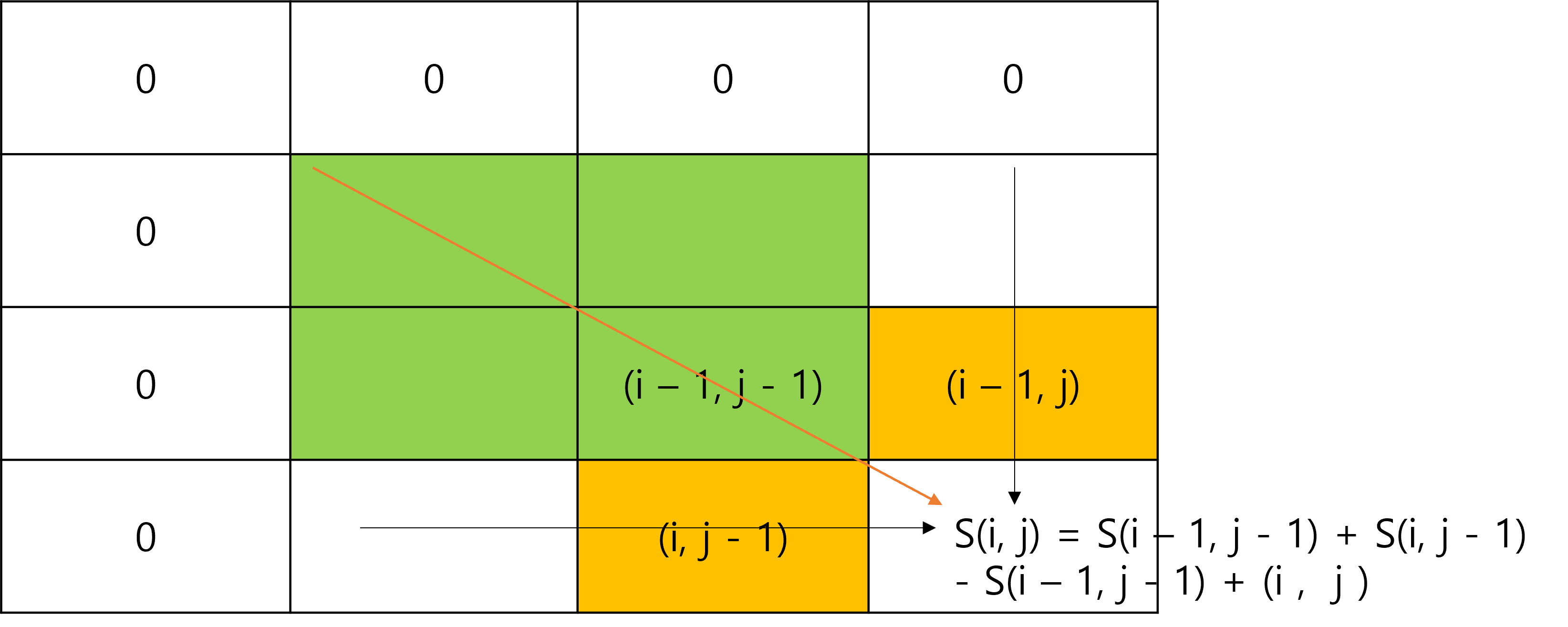
위 그림으로 보면 (i, j)의 누적합은 (i - 1, j)의 누적합과 (i , j -1)까지의 누적합을 더 하고 (i - 1, j), (i , j -1) 공통 되는
(i - 1, j -1) 누적합을 빼면 된다. 이해가 안 되면 합집합의 이론을 생각 해보면 된다. 맨 위하고 맨 왼쪽에 0을 추가하는 이유는 (1, 1 ~ n), (1 ~ n, 1)부분을 연산하기 위해서다. 코드 상에 맨위 맨 왼쪽 계산 할때 IndexErro 가 나오고 예외로 코드 작성하기는에는 몇 줄이 추가 되기 때문이다.
Code
Python
matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
size = len(matrix)
prefix_sum = [[0] * (size + 1) for _ in range(size + 1) ]
for i in range(1, size + 1):
for j in range(1, size + 1):
#prefix_sum(i, j) = matrix(i, j) + prefix_sum(i - 1, j) + prefix_sum(i, j - 1) - prefix_sum(i - 1, j - 1)
prefix_sum[i][j] = matrix[i - 1][j - 1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i -1][j - 1]Java
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
int size = matrix.length;
int[][] prefix_sum = new int[size + 1][size + 1];
for(int i = 1; i <= size; i++) {
for(int j = 1; j <= size; j++) {
// prefix_sum(i, j) = matrix(i, j) + prefix_sum(i - 1, j) + prefix_sum(i, j - 1) - prefix_sum(i - 1, j - 1)
prefix_sum[i][j] = matrix[i - 1][j - 1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i - 1][j - 1];
}
}
Arrays.stream(prefix_sum).forEach(array -> System.out.println(Arrays.toString(array)));
}
}구간합
위에 2차원 배열 누적합의 원리에 대해서 이해 했다면 구간합도 이해할수 있을거라 생각한다. 1차원 배열일때 x1 ~ x2의 구간합은 x2의 누적합과 x1 - 1의 누적합의 빼면 됬다. 2차원 배열은 1차원 배열에서 합집합의 개념을 추가 했다고 보면 된다.
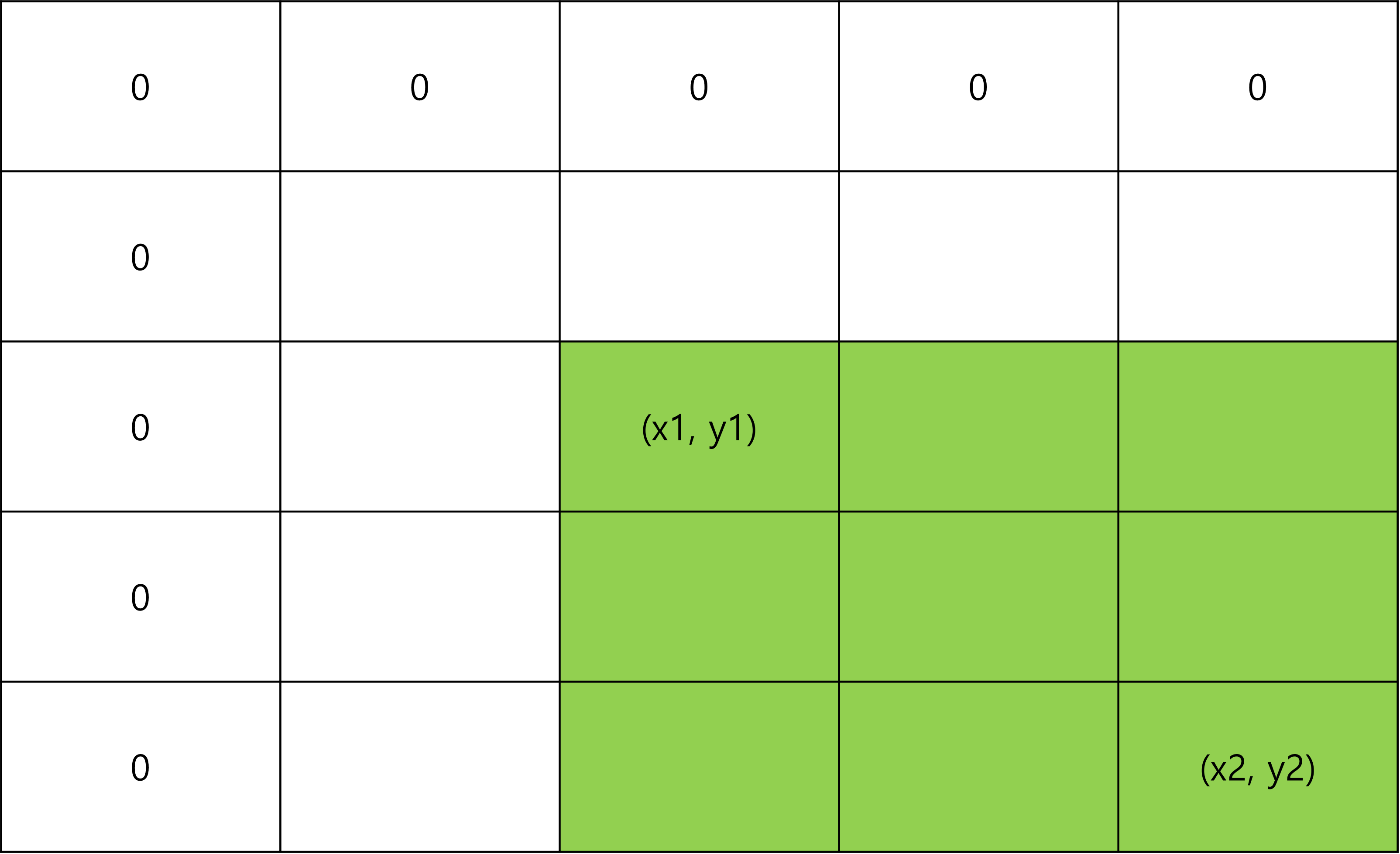
위에 표는 (x1, y1) 부터 (x2, y2)의 합을 영역 표시한것이다. 이 영역을 누적합적용할라면 (x1, y1)의 누적합과 (x2, y2)의 공통 되는 영역을 제거하면된다.
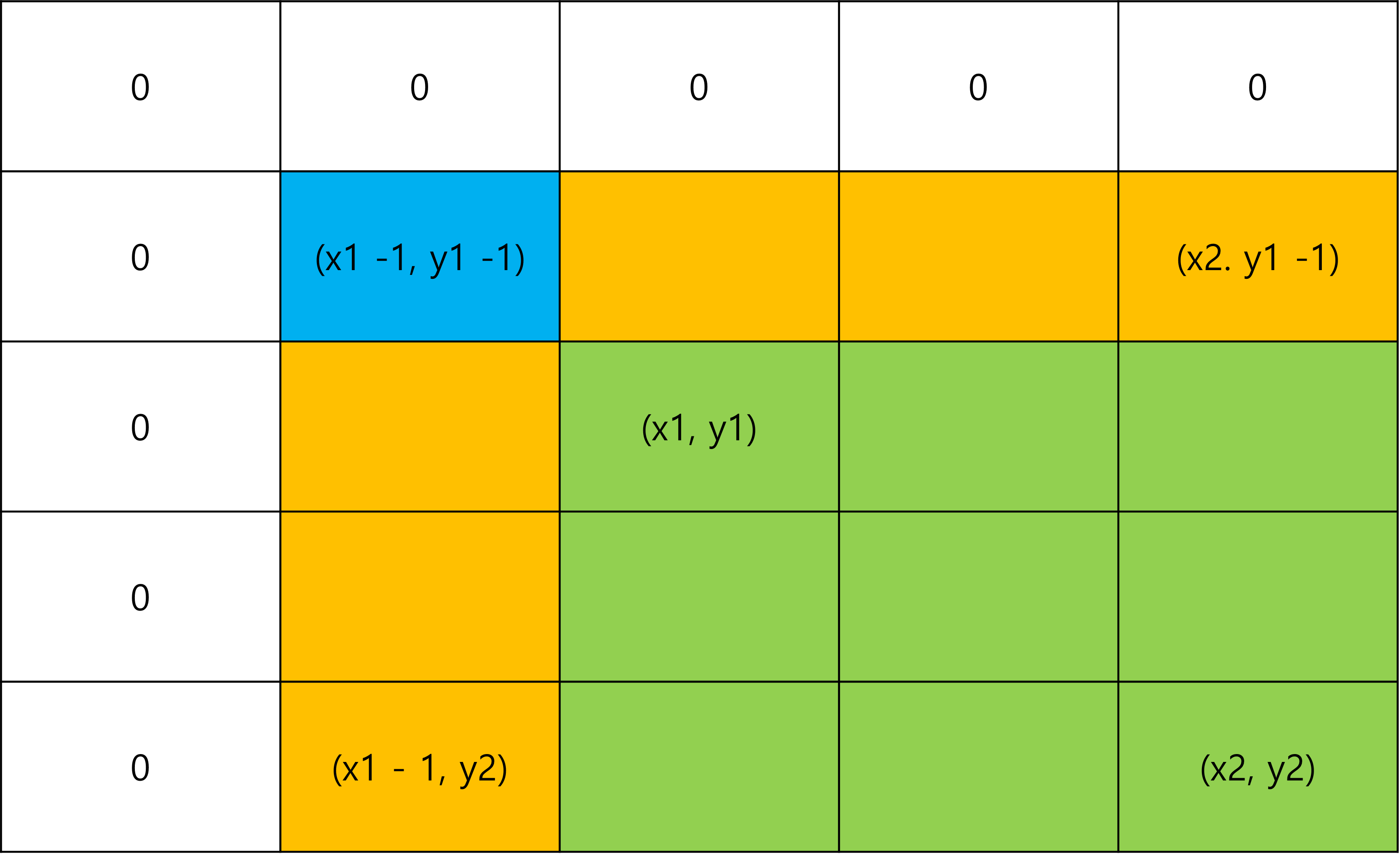
위 그림을 보면 주항색은 공통된 영역이다. 공통된 영역인 (x1 - 1, y2)와 (x2, y1 -1)의 누적합을 빼주면 된다.
하지만 (x1 -1, y - 1)만 파란색으로 했다 그 이유는 (x1 - 1, y2)와 (x2, y1 -1)의 누적합한 부분이 (x1 -1, y - 1) 공통으로 들어있어서 2번을 빼는 경우가 생긴다. 그래서 파란색 영역을 다시 더해줘야 (x1, y1), (x2, y2)의 공통영역을 제거 할 수가 있다.
다시 정리한다면 아래의 식 처럼 표현 할수가 있다.
Range(x1, y1, x2, y2) = S(x2, y2) - S(x2, y1 -1) - S(x1 - 1, y2) + S(x1 - 1 , y1 -1)
Code
Python
matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
size = len(matrix)
prefix_sum = [[0] * (size + 1) for _ in range(size + 1) ]
for i in range(1, size + 1):
for j in range(1, size + 1):
#prefix_sum(i, j) = matrix(i, j) + prefix_sum(i - 1, j) + prefix_sum(i, j - 1) - prefix_sum(i - 1, j - 1)
prefix_sum[i][j] = matrix[i - 1][j - 1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i -1][j - 1]
x1, y1, x2, y2 = 2, 1, 3, 4
Range_value = prefix_sum[x2][y2] + prefix_sum[x1 -1][y1 -1] - prefix_sum[x2][y1 - 1] - prefix_sum[x1 - 1][y2]Java
public class Main {
public static void main(String[] args) {
int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
int size = matrix.length;
int[][] prefix_sum = new int[size + 1][size + 1];
for(int i = 1; i <= size; i++) {
for(int j = 1; j <= size; j++) {
// prefix_sum(i, j) = matrix(i, j) + prefix_sum(i - 1, j) + prefix_sum(i, j - 1) - prefix_sum(i - 1, j - 1)
prefix_sum[i][j] = matrix[i - 1][j - 1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i - 1][j - 1];
}
}
int x1 = 2;
int y1 = 1;
int x2 = 4;
int y2 = 3;
int RangeValue = prefix_sum[x2][y2] + prefix_sum[x1 -1][y1 -1] - prefix_sum[x2][y1 - 1] - prefix_sum[x1 - 1][y2];
}
}2차원 구간합, 누적합 추천 문제
문제: 구간 합 구하기 5
난이도: 하
가장 기본적인 문제이다. 풀어보는것 추천한다.
https://www.acmicpc.net/problem/11660
'알고리즘 > 이론' 카테고리의 다른 글
| [알고리즘 이론] 백트래킹(Backtracking) (0) | 2022.12.09 |
|---|---|
| [알고리즘 이론] 힙(Heap) (0) | 2022.12.07 |
| [알고리즘 이론] 그리디(Greedy) (0) | 2022.11.23 |
| [알고리즘 이론] LIS(Longest Increasing Subsequence) 최장 증가 부분 수열 (0) | 2022.11.02 |
| 유클리드 호제법(Euclidean algorithm) (0) | 2022.09.21 |
