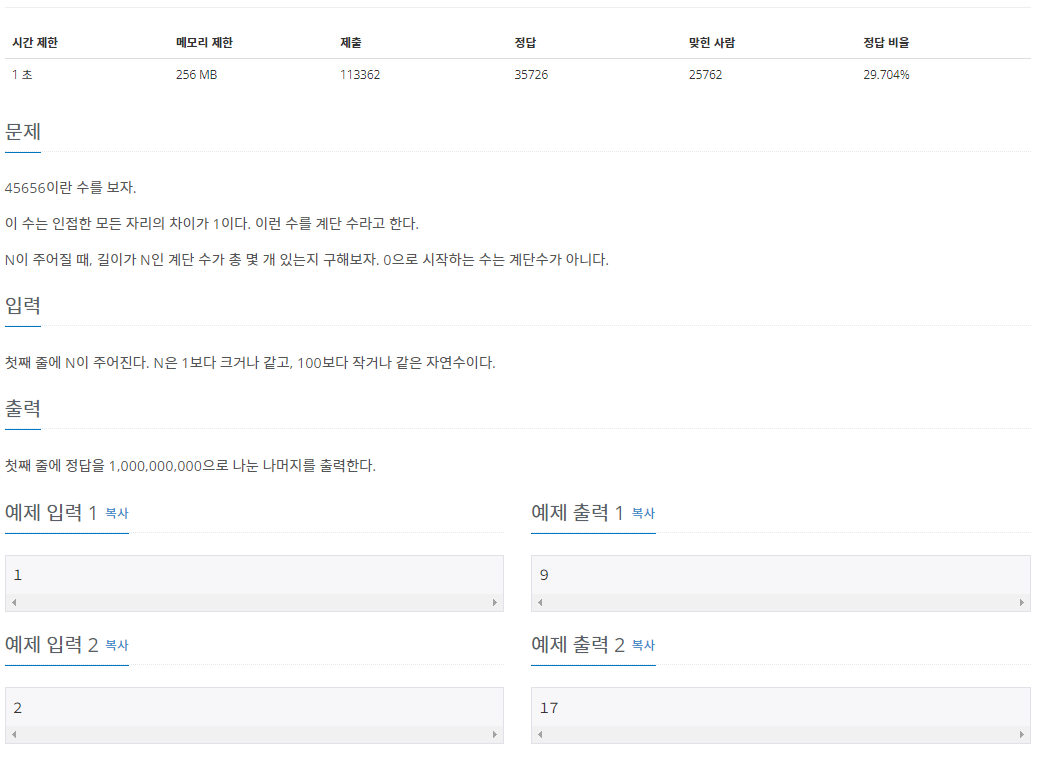
문제 요악
- 알고리즘 분류: 동적 계획법
- 난이도: Silver1
- 문제 요약
- 숫자 앞뒤 차이가 1인 수는 계단수이다.
- 숫자 길이가 N 으로 주어졌을때 길이 N 수인중에 계단수를 구해라
- 사이트 주소: https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
문제 풀이
동적 계획법 관련 내용은 아래 사이트에 참조 하면된다.
https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95
동적 계획법 - 나무위키
동적 계획법의 개념과 구현에 대해 정확하게 짚고 넘어가기 위해 동적 계획법을 적용시킬 수 있는 예에 대해 알아보자. f(a,b) = f(a-1,b) + f(a,b-1) (a,b >= 1 )f(0,0) = 1, 임의의 자연수 n에 대해 f(n,0) = f(0,
namu.wiki
문제 접근 방법
위에 문제가 N이 최대 100이라고 되어있다. 길이가 100인 수는 즉 10의 100승의 수를 탐색할려면 시간이 초과가 된다.
그래서 규칙을 파악해서 길이가 1부터 100까지만 탐색하도록 구현 해야 한다.
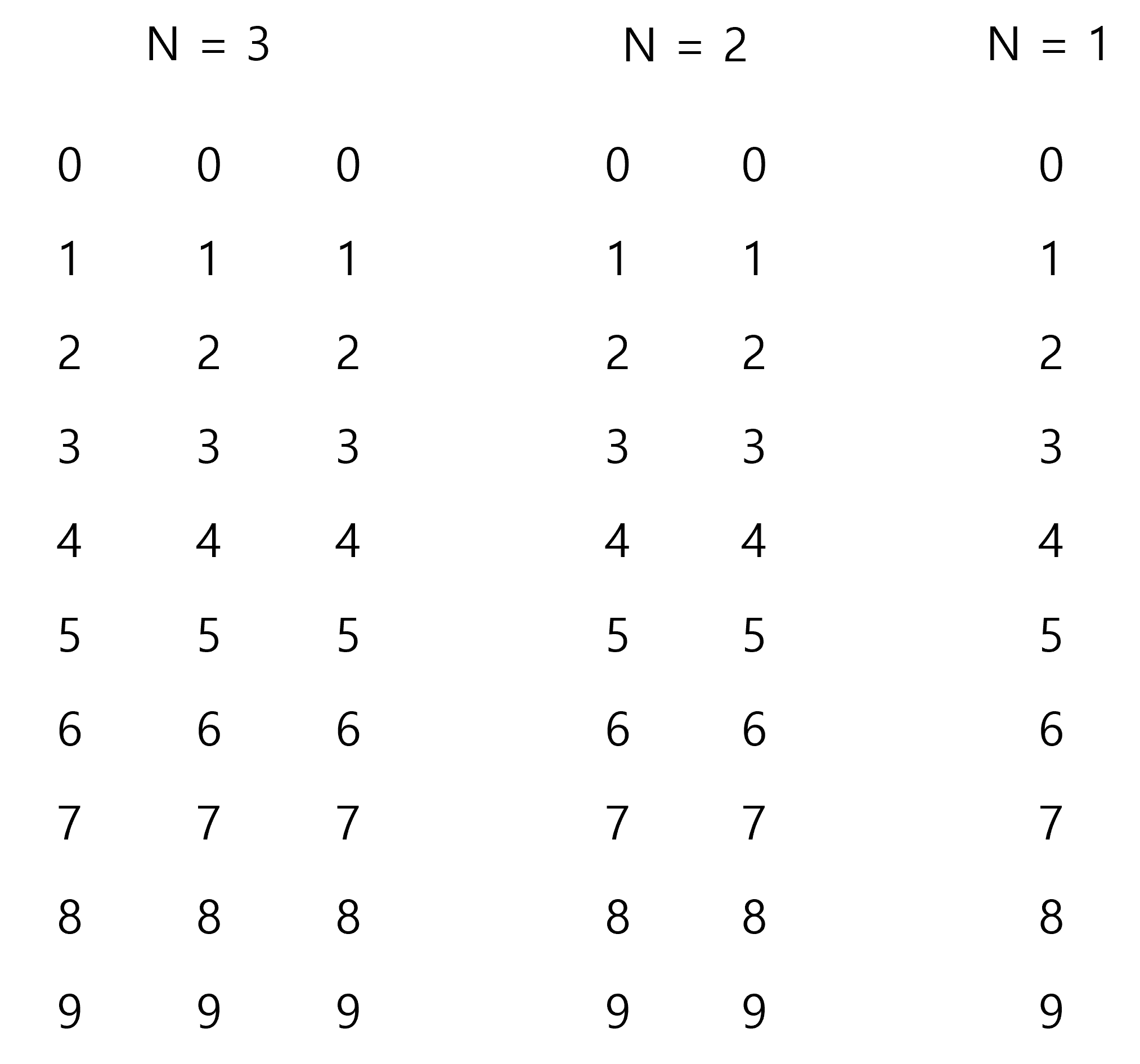
위 의 그림을 길이 만큼 표로 나타낸것이다. N = 1 일때 0을 제외하면 각 수의 경우 수는 1이 나온다.
N = 2일때는 01, 10, 12 , 21, 23, 32, 34.... 이다.
N = 3일때는 012, 010, 101, 121, 123, 210, 212, 232, 234, 321, 323, 343, 345.... 가 있다
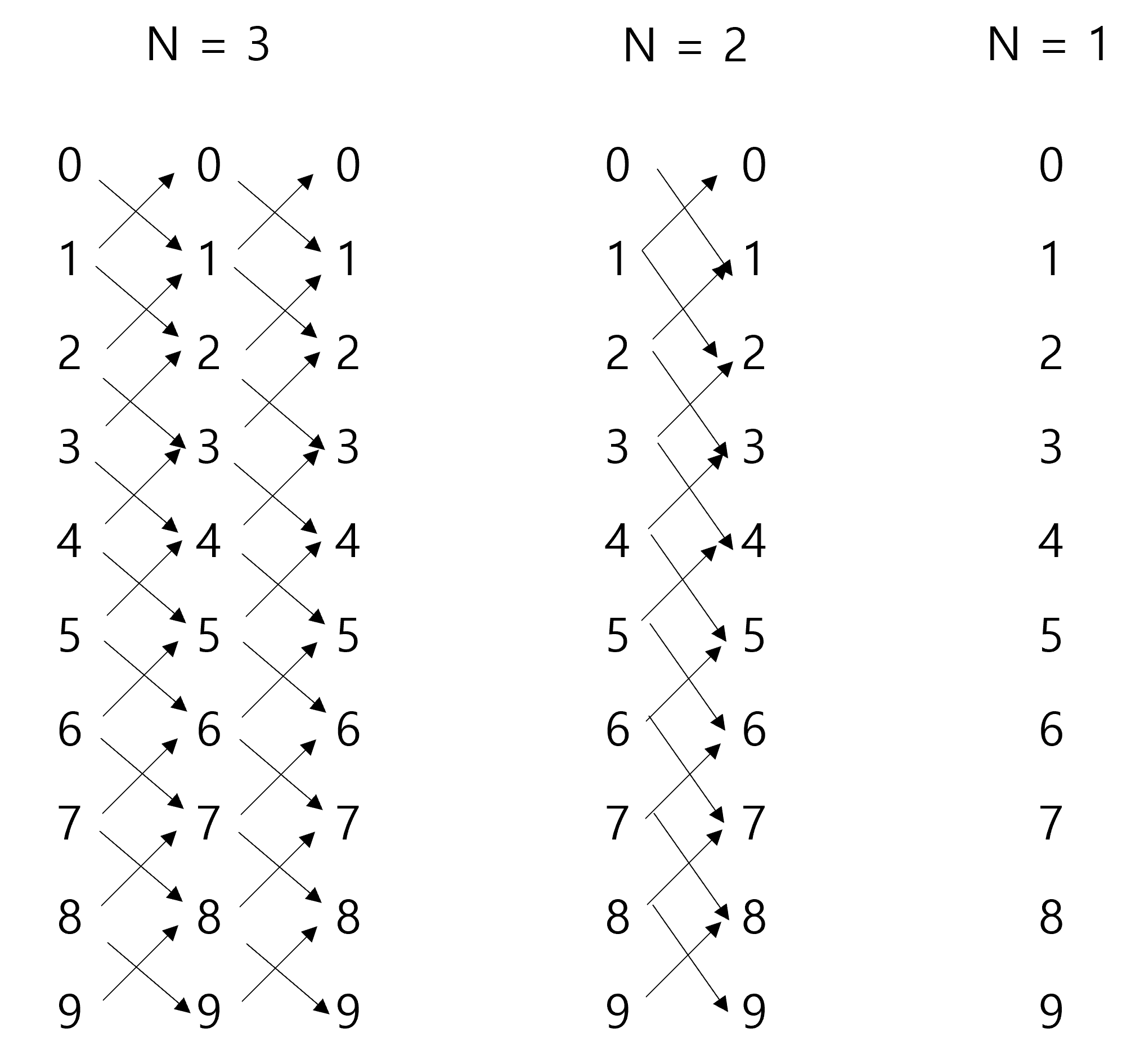
다시 그림을 보면 각 수의 그 뒤에 나올수 있는 수가 뭐가 나오는지 화살표로 표현을 했다. n = 1 일때는 0을 제외하면 뒤에 숫자가 없어서 각 0이다. n = 2일때는 첫번째 자리수를 보면 0, 9를 제외하면 뒤에 나올수 있는 수는 ±1이다. 0은 뒤에 올수 있는 숫자는 1, 9가 뒤에 올 수 있는 수는 8이다. n = 3 일때는 첫번째 자리에서 0, 9를 제외하면 두 번째 자리에서 ±1수가 올수 있다. 두 번 자리에서는 셋번째 자리에서 ±1수가 올수 있다.

N = 4 일 경우에도 그림 으로 보면 N의 3일때 경의수를 추가해서 첫번째 자리수를 0, 9를 제외 하면 ±1수가 오는 경우를 추가만 해주면 된
다. 위에 그림 을 식으로 표현 하면 아래와 같은 공식이 나온다.

이 공식을 코드로 표현만 하면 된다.
Code
Python
n = int(input())
dp = [[1] * (10) for _ in range(n + 1)]
dp[0][0], dp[1][0] = 0, 0
MOD = 1000000000
for i in range(2, n + 1):
dp[i][0] = dp[i - 1][1]
for j in range(1, 9):
dp[i][j] = (dp[i-1][j-1] + dp[i-1][j + 1]) % MOD
dp[i][9] = dp[i - 1][8]
print(sum(dp[n][1:]) % MOD)Java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
long MOD = 1000000000;
long dp[][] = new long[n+1][10];
Arrays.setAll(dp[1], i -> 1);
dp[1][0] = 0;
for(int i = 2; i <= n; i++) {
dp[i][0] = dp[i-1][1];
for(int j = 1; j<=8; j++) {
dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % MOD;
}
dp[i][9] = dp[i-1][8];
}
System.out.println(Arrays.stream(dp[n]).sum() % MOD);
}
}'알고리즘 > 백준' 카테고리의 다른 글
| [BAEKJOON] 2565 전깃줄 (0) | 2022.11.03 |
|---|---|
| [BAEKJOON] 2156 포도주 시식 (1) | 2022.11.01 |
| [BAEKJOON] 1932 정수 삼각형 (0) | 2022.10.28 |
| [BAEKJOON] 1912 연속합 (0) | 2022.10.27 |
| [BAEKJOON] 9184 신나는 함수 실행 (0) | 2022.10.26 |



