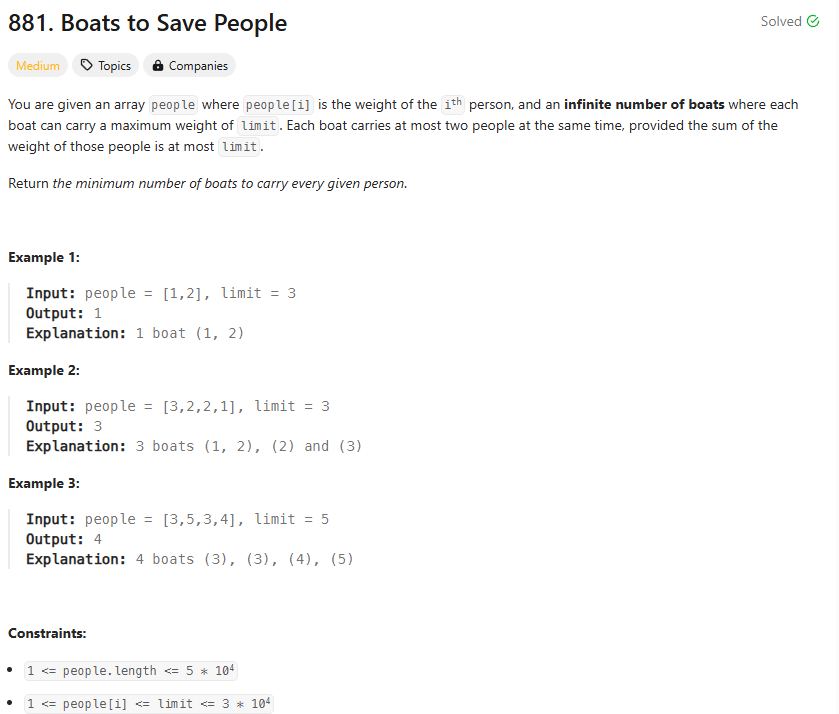
문제 요약
- 알고리즘 분류: 그리디, 투 포인터, 정렬
- 난이도: Medium
- 문제내용:
- 각 보트는 최대 2명까지만 태울 수 있습니다.
- 보트에 태운 사람들의 몸무게 합은 limit를 초과할 수 없습니다.
- 모든 사람을 태우기 위한 최소 보트 수를 구해야 합니다.
- 사이트 주소: https://leetcode.com/problems/boats-to-save-people/description/
문제풀이
이번 문제에서는 완전탐색으로 풀수 있지만 최대 크기가 10^5인점으로 고려하면 다른 방법으로 풀어야 한다. 그래서 이번에는 그리디와 투 포인트로 풀어야 한다. 그에 대한 이론 설명은 아래 글에 확인 해보면 됩니다.
[알고리즘 이론] 투 포인터(Two Pointers)
설명은 나중에 올리겠다.
jih3508.tistory.com
문제 접근 방법
그리디 알고리즘
그리디 알고리즘은 각 단계에서 최적의 선택을 하는 방식으로 문제를 해결합니다. 이 문제에서는 "최소한의 보트로 모든 사람을 태우기" 위해 가능한 한 각 보트에 두 명씩 태우는 것이 최적입니다. 그리고 그 중에서도 가장 무거운 사람과 가장 가벼운 사람을 함께 태우는 전략이 효과적입니다.
투 포인터 기법
투 포인터 기법은 배열의 두 요소를 가리키는 두 개의 포인터를 사용하여 문제를 해결하는 방법입니다. 이 문제에서는:
- start 포인터: 가장 가벼운 사람부터 시작 (배열의 시작점에서 시작)
- end 포인터: 가장 무거운 사람부터 시작 (배열의 끝점에서 시작)
이 두 포인터를 사용하여 양쪽에서 동시에 배열을 순회하며 최적의 조합을 찾습니다.
투 포인터 기법 심층 분석
이 문제에서 투 포인터 기법이 특히 효과적인 이유는 다음과 같습니다:
1. 최적의 조합 찾기
투 포인터 기법은 정렬된 배열에서 특정 조건을 만족하는 요소 쌍을 찾는 데 매우 효과적입니다. 이 문제에서는 가장 가벼운 사람과 가장 무거운 사람의 조합을 고려함으로써:
- 가장 무거운 사람은 어차피 한 보트에 한 명만 태울 가능성이 높습니다.
- 가장 가벼운 사람은 다른 사람과 함께 태울 가능성이 높습니다.
- 이 두 사람을 함께 태울 수 있다면, 이는 최적의 조합입니다.
2. 선형 시간 복잡도
두 포인터를 사용하면 단일 패스(O(n))로 모든 사람을 처리할 수 있습니다. 이는 다른 조합을 모두 시도하는 것보다 훨씬 효율적입니다.
3. 포인터 이동 전략
- start가 증가하는 경우: 가장 가벼운 사람이 보트에 태워집니다.
- end가 감소하는 경우: 가장 무거운 사람이 보트에 태워집니다.
이 전략을 통해 각 단계에서 최적의 선택을 할 수 있습니다:
- 두 사람을 함께 태울 수 있을 때: 가장 가벼운 사람과 가장 무거운 사람을 함께 태워 보트를 최대한 활용합니다.
- 한 사람만 태울 수 있을 때: 가장 무거운 사람부터 태워 나머지 사람들의 조합 가능성을 높입니다.
구현 방법
최적의 해결책을 찾기 위한 방법은 다음과 같습니다:
- 먼저 모든 사람을 몸무게 순으로 정렬합니다.
- 두 개의 포인터를 설정합니다: start는 배열의 시작, end는 배열의 끝을 가리킵니다.
- 두 포인터가 가리키는 사람들을 함께 태울 수 있는지 확인합니다:
- 두 사람의 무게 합이 limit 이하라면, 두 사람을 한 보트에 태우고 두 포인터를 모두 이동시킵니다(start++, end--).
- 두 사람의 무게 합이 limit를 초과한다면, 가장 무거운 사람만 보트에 태우고 end 포인터만 이동시킵니다(end--).
이러한 투 포인터 접근 방식은 모든 사람을 한 번씩만 확인하면서 최소한의 보트를 사용할 수 있게 합니다.
마무리
투 포인터와 그리디 알고리즘의 결합
이 문제에서 투 포인터와 그리디 알고리즘의 결합이 왜 효율적인지 살펴보겠습니다:
- 그리디의 관점: 각 단계에서 최적의 결정을 내리는 그리디 전략은 "가능한 한 많은 사람을 한 보트에 태우는 것"입니다. 보트가 최대 2명까지 태울 수 있으므로, 이상적으로는 모든 보트에 2명씩 태우는 것이 최적입니다.
- 투 포인터의 역할: 투 포인터 기법은 이러한 그리디 전략을 효과적으로 구현하는 도구입니다. 정렬된 배열에서 양 끝의 값을 조합하여 최적의 구성을 찾아냅니다.
- 최적성 증명:
- 정렬된 배열에서 가장 무거운 사람(end)을 먼저 고려합니다.
- 이 사람은 어차피 한 보트에 태워야 합니다.
- 이 사람과 함께 태울 수 있는 가장 가벼운 사람(start)이 있다면, 이는 최적의 조합입니다.
- 함께 태울 수 없다면, 무거운 사람만 태우는 것이 최선입니다.
이러한 방식으로 투 포인터 기법은 그리디 알고리즘의 핵심 아이디어를 효율적으로 구현하는 데 사용됩니다.
이 문제는 그리디 알고리즘과 투 포인터 기법을 결합하여 효율적으로 해결할 수 있습니다. 정렬된 배열에서 가장 가벼운 사람과 가장 무거운 사람을 동시에 고려하는 투 포인터 방식을 통해 최소한의 보트를 사용하여 모든 사람을 구출할 수 있습니다.
시간 복잡도에서는 정렬에 O(n log n) 순회 하는데 O(n)이 걸립니다. 그래서 위 구현의 시간 복잡도는 O(nlogn) 만큼 소요 됩니다.
Code
Python
class Solution:
def numRescueBoats(self, people: List[int], limit: int) -> int:
# 사람들의 몸무게를 오름차순으로 정렬
people.sort()
count = 0 # 필요한 보트 수
start,end = 0, len(people) - 1
while start <= end:
# 가장 가벼운 사람과 가장 무거운 사람의 몸무게 합이 limit 이하인 경우 두 사람을 한 보트에 태웁니다
# 두 사람의 몸무게 합이 limit를 초과하는 경우 가장 무거운 사람만 보트에 태웁니다
if people[start] + people[end] <= limit:
start ,end = start + 1, end - 1
else:
end -= 1
count += 1 # 사용한 보트 수를 증가
return count
Java
class Solution {
public int numRescueBoats(int[] people, int limit) {
// 사람들의 몸무게를 오름차순으로 정렬
Arrays.sort(people);
int count = 0; // 필요한 보트 수
int start = 0;
int end = people.length - 1;
while(start <= end){
// 가장 가벼운 사람과 가장 무거운 사람의 몸무게 합이 limit 이하인 경우 두 사람을 한 보트에 태웁니다
// 두 사람의 몸무게 합이 limit를 초과하는 경우 가장 무거운 사람만 보트에 태웁니다
if(people[start] + people[end--] <= limit){
start++;
}
count++; // 사용한 보트 수를 증가
}
return count;
}
}Javascript
var numRescueBoats = function(people, limit) {
// 사람들의 몸무게를 오름차순으로 정렬
people.sort(function (a, b) {
return a - b;
});
let count = 0; // 필요한 보트 수
let start = 0;
let end = people.length - 1;
while(start <= end){
// 가장 가벼운 사람과 가장 무거운 사람의 몸무게 합이 limit 이하인 경우 두 사람을 한 보트에 태웁니다
// 두 사람의 몸무게 합이 limit를 초과하는 경우 가장 무거운 사람만 보트에 태웁니다
if(people[start] + people[end--] <= limit){
start++;
}
count++; // 사용한 보트 수를 증가
}
return count;
};'알고리즘 > Leetcode' 카테고리의 다른 글
| [Leetcode]1306. Jump Game III (0) | 2025.05.07 |
|---|---|
| [Leetcode] 3016. Minimum Number of Pushes to Type Word II (0) | 2025.05.06 |
| [Leetcode] 1833. Maximum Ice Cream Bars (1) | 2025.04.23 |
| [Leetcode] 802. Find Eventual Safe States (2) | 2025.04.22 |
| [Leetcode]554. Brick Wall (0) | 2025.04.15 |



